Any INFJs that are good at maths?

The answers are not foggy, so I like being right or wrong if someone can show me why it was wrong.
 
I hate math. Had I learned to love it the way I love other subjects...no doubt I would have become a surgeon. An award winning one cause why not?
 
Maikl Jexocuha said:
View attachment 76244
Click to expand...
If it's taught badly and people don't practice then sure. That's why school funding, especially public school funding is so important.

Kids shouldn't have to deal with overcrowded class rooms and shitty teachers. There should also be more opportunities for 1:1 attention in schools.
 
InfernoMink said:
You guys have made me change my mind. I don't hate math. I'm just lazy. I feel better now.
Click to expand...
You might not be lazy, you might not just have the energy for practicing it in light of the other things you might have to do in a day. You also might not have been taught math well. That's not your fault.

If what I said offends you I'm sorry but I don't know how to say it in a nicer way because I'm not blaming you for your math performance. Good or bad.
 
Pin said:
You might not be lazy, you might not just have the energy for practicing it in light of the other things you might have to do in a day. You also might not have been taught math well. That's not your fault.

If what I said offends you I'm sorry but I don't know how to say it in a nicer way because I'm not blaming you for your math performance. Good or bad.
Click to expand...
You hit the nail on the proverbial head. My mother was no math genius. She could not explain it to me. I used to get hit because I didn't get it and she had things to do. When it comes to fancy math i dont know what happens but I just shut the f down. lol.
 
I was always good at math. When I took the SAT, I finished above 99% (highest you could finish) and thought I might have aced it (gotten everything right).

Here is a wonderfully elegant math problem:

A boat is twice as old as its engine was when the boat was as old as its engine is. Find the ratio of the age of the engine to the boat.
 
o2b said:
I was always good at math. When I took the SAT, I finished above 99% (highest you could finish) and thought I might have aced it (gotten everything right).

Here is a wonderfully elegant math problem:

A boat is twice as old as its engine was when the boat was as old as its engine is. Find the ratio of the age of the engine to the boat.
Click to expand...
So jealous. No doubt about it, if math came easy to me, I would have pursued becoming a Pediatrician. Maybe in my next lifetime.
 
o2b said:
Here is a wonderfully elegant math problem:

A boat is twice as old as its engine was when the boat was as old as its engine is. Find the ratio of the age of the engine to the boat.
Click to expand...
The wording on this confused me a moment.
If the boat is 8 years old, and its engine 6 years old, then when the boat was 6 years old its engine would've been 4 years old.
I don't remember how to express ratios (might've never learned?). Would it be written like, 3:4 (current engine age to current boat age)?
 
Winterflowers said:
The wording on this confused me a moment.
If the boat is 8 years old, and its engine 6 years old, then when the boat was 6 years old its engine would've been 4 years old.
I don't remember how to express ratios (might've never learned?). Would it be written like, 3:4 (current engine age to current boat age)?
Click to expand...
That is the correct answer! 3/4.

I would love to see how you arrived at the answer. I'll show how I arrived at it at some point.

Thanks!
 
What the heck. I'll do it now. This is a very elegant algebraic problem.

A boat is twice as old as its engine was when the boat was as old as its engine is. Find the ratio of the age of the engine to the boat.

Problem Setup:

|----------- |Boat | Engine |
| - Was - | - w --| ---- x ----|

| --- Is -- | - y -- | ---- z ----|

So far so good, right?

Substitution 1:

A boat is twice as old as its engine was. Boat(is) = 2xEngine(was). So y=2x.

|----------- |Boat | Engine |
| - Was - | - w --| ---- x ----|

| --- Is -- | - 2x - | ---- z ----|


Substitution 2:

When the boat was as old as its engine is. Boat(was) = Engine(is). So w=z.

|----------- |Boat | Engine |
| - Was - | - z --| ---- x ----|

| --- Is -- | - 2x - | ---- z ----|


What are we supposed to solve?

Find the ratio of the age of the engine to the boat. Find z/2x


Recognize Equivalence:

Boat(is) - Boat(was) = Engine(is) - Engine(was)

2x - z = z - x


Solve for z/2x:

2x - z = z - x

3x = 2z

z/2x = (3/2)/2

z/2x = 3/4
 
Last edited:
o2b said:
What the heck. I'll do it now. This is a very elegant algebraic problem.

A boat is twice as old as its engine was when the boat was as old as its engine is. Find the ratio of the age of the engine to the boat.

Problem Setup:

|----------- |Boat | Engine |
| - Was - | - w --| ---- x ----|

| --- Is -- | - y -- | ---- z ----|

So far so good, right?

Substitution 1:

A boat is twice as old as its engine was. Boat(is) = 2xEngine(was). So y=2x.

|----------- |Boat | Engine |
| - Was - | - w --| ---- x ----|

| --- Is -- | - 2x - | ---- z ----|


Substitution 2:

When the boat was as old as its engine is. Boat(was) = Engine(is). So w=z.

|----------- |Boat | Engine |
| - Was - | - z --| ---- x ----|

| --- Is -- | - 2x - | ---- z ----|


What are we supposed to solve?

Find the ratio of the age of the engine to the boat. Find z/2x


Recognize Equivalence:

Boat(is) - Boat(was) = Engine(is) - Engine(was)

2x - z = z - x


Solve for z/2x:

2x - z = z - x

3x = 2z

z/2x = (3/2)/2

z/2x = 3/4
Click to expand...
Algebra isn't my strong area though the way you write it out makes it look easier.
I tried mapping it out like that in my head but felt too hazy (no sleep). So I visualized two objects accelerating and assigned numbers to them. And I don't remember the rest but it fell into place after that.
 
Winterflowers said:
Algebra isn't my strong area though the way you write it out makes it look easier.
I tried mapping it out like that in my head but felt too hazy (no sleep). So I visualized two objects accelerating and assigned numbers to them. And I don't remember the rest but it fell into place after that.
Click to expand...
Of all places, I saw the problem in some Christian forum. These two guys were bickering and one guy told the other he probably could not solve this math problem (yeah, pretty weird).

Took me maybe 25 minutes, but I think I was lucky. I think the hardest parts are the setup and realizing that the is minus was time increments between engine and boat must be the same.

Notice that the ages cannot be determined. There is not enough information. The ratio of z to x may be known, but not their individual values.

I have given this problem to various folks over the years, including a guy with a masters degree at MIT for some science discipline. I have yet to see anyone get as far as properly setting it up. A couple got it like you did, intuitively, I suppose.
 
o2b said:
Of all places, I saw the problem in some Christian forum. These two guys were bickering and one guy told the other he probably could not solve this math problem (yeah, pretty weird).

Took me maybe 25 minutes, but I think I was lucky. I think the hardest parts are the setup and realizing that the is minus was time increments between engine and boat must be the same.

Notice that the ages cannot be determined. There is not enough information. The ratio of z to x may be known, but not their individual values.

I have given this problem to various folks over the years, including a guy with a masters degree at MIT for some science discipline. I have yet to see anyone get as far as properly setting it up. A couple got it like you did, intuitively, I suppose.
Click to expand...
Two guys were bickering on a Christian forum... (this sounds like a joke setup, haha)

And 25 minutes. Why do you think it was lucky?
For me the wording was just turning me around. But I was near passing out too and looking back now it seems somewhat clearer (that could also be from having worked through it though).
Setting it up seemed more challenging to me than solving for your answer ^_^ it's neat how you laid it all out.
 
As far as lucky, mainly thinking of the setup part. Dividing it into boat(was), boat(is), etc. and just assigning variables.
 
o2b said:
I was always good at math. When I took the SAT, I finished above 99% (highest you could finish) and thought I might have aced it (gotten everything right).

Here is a wonderfully elegant math problem:

A boat is twice as old as its engine was when the boat was as old as its engine is. Find the ratio of the age of the engine to the boat.
Click to expand...
Great problem o2b. I've had a go before looking at yours and @Winterflowers solutions in detail - see if I can de-rust my maths ;). This is how it came out:

upload_2021-8-28_22-14-49.png

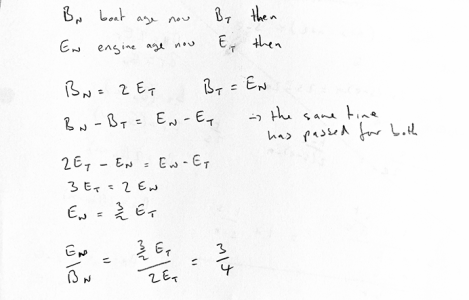
What held me up for a while is the importance of line 4. It seems to state the obvious, but it's the critical algebraic link that binds the information together. I'll backtrack now and see how this compares with your solutions.

{Edit: Yayyy! Same answer and very similar solution to yours o2b}
 
You must log in or register to reply here.
Back
Top